Simulation and Research Methodology for the Process of Conveying Bulk Materials by Screw Conveyors

Full Text

Введение

Зерноуборочный комбайн является одним из основных средств механизации в процессе уборки зерновых культур. На эффективность процесса выгрузки из бункера комбайна убранного урожая большое влияние оказывают физико-механические свойства зернового вороха и геометрические, кинематические параметры выгрузного устройства. Нарушения в технологическом процессе выгрузки приводят к остановке всего процесса уборки, простою комбайна, увеличению сроков уборки и дополнительным потерям урожая.

Шнековые транспортеры являются одними из эффективных рабочих органов, обладающих высокой степенью надежности выполнения технологического процесса транспортирования, что обуславливает их разностороннее применение, в том числе и в зерноуборочных комбайнах. Система транспортирования зернового материала внутри зерноуборочного комбайна, а также процесс его выгрузки является важной частью работы комбайна. В зависимости от геометрических и конструктивных параметров, кинематических режимов функционирования формируется эффективность его работы, определяются качественные и количественные характеристики процесса транспортирования, а именно повреждения транспортируемого материала, мощность, расходуемая на его перемещение, и затраты энергии на транспортировку. Также при работе на повышенных скоростях и нагрузках происходит высокий износ как элементов шнековых транспортеров, так и их привода, что может приводить к поломкам, провоцирующим простой техники и снижение маржинальности всего технологического процесса производства продукции растениеводства.

Для моделирования и исследования процесса перемещения сыпучей среды шнековыми транспортерами необходимо создание цифровых моделей систем транспортирования, проведение сравнительного анализа их функционирования и последующая оптимизация их работы под конкретные характеристики технологического процесса с учетом широкой вариации технологических свойств сыпучей среды, поступающей на транспортировку. Данные методики позволяют более глубоко проводить анализ процесса транспортировки за счет наблюдения за визуализацией работы его цифрового двойника и получения цифровой информации о процессе и последующей его оптимизации.

В качестве критерия эффективности процесса перемещения предлагается использовать мощность, необходимую для перемещения заданного материала. Однако существующие методики по определению необходимой мощности не учитывают ряд параметров, связанных с широкой вероятностью свойств сыпучей среды, поступающей на транспортирование, различиями траекторий каждой отдельно взятой транспортируемой частицы (форма частиц, размерные характеристики, наличие примесей, фракционного состава, взаимоперемещение материала внутри системы) и с потерями, связанными с внутренним трением частиц друг об друга и колебанием материала относительно гравитационных сил. Нами предлагается усовершенствованная методика, позволяющая учесть данные факторы при создании новых и оптимизации уже существующих шнековых систем транспортирования.

Целью исследования является разработка и обоснование методики, позволяющей оценивать эффективность работы шнековых систем транспортирования в зависимости от свойств транспортируемой сыпучей среды.

Обзор литературы

Транспортировка продуктов в шнековых устройствах представляет сложный процесс, поэтому его математическое описание довольно затруднительно.

На стадии проектирования производительность шнеков принято определять в большинстве случаев, используя зависимость¹:

                                          

где D – наружный диаметр винта, м; d – диаметр вала винта, м; λ – радиальный зазор между наружной кромкой винта и внутренней поверхностью кожуха шнека, м; S – шаг витков, м; ψ – коэффициент заполнения; n – число оборотов винта в минуту; γ – объемный вес перемещаемого материала, т/м³; c – коэффициент снижения производительности в зависимости от наклона шнека.

Существующая модель дает достаточно приближенные значения, так как не учитывает существенное количество конструктивных параметров шнековых транспортеров и свойств транспортируемой сыпучей среды (коэффициент трения сыпучей среды о поверхность трубы, вала и спирали шнека; коэффициенты статического и динамического трения частиц сыпучей среды; силы адгезии, действующие между частицами и между частицами и поверхностью; диссипативные силы взаимодействия; наличие примесей других частиц; форма частиц и т. д.), отдельное и совокупное влияние которых существенно изменяет процесс транспортирования.

При проектировании шнековые транспортеры принято разделять условно на четыре группы в зависимости от угла наклона: горизонтальные, имеющие малый наклон (до 20°), имеющие большой наклон к горизонту (от 20° до 90°) и вертикальные. В настоящее время существуют стандарты для винтовых конвейеров: ГОСТ 2037-82², DIN 15261 в двух частях³, DIN 15262-1983⁴ – эквивалент стандарта ISO 7119-1981⁵. Данные стандарты имеют различные методики для расчета параметров шнековых транспортеров.

Исследованием процесса транспортирования занимались следующие ученые: О. А. Старовойтова и др. [1] занимались описанием физического процесса движения корнеплодов в вертикальном шнеке; З. А. Меретукова и др. [2; 3] определением производительности транспортера со спиральным шнеком; Л. Г. Крючкова [4] вычислением потребляемой мощности на процесс транспортирования; Д. С. Беленко и А. Б. Мишин [5] исследовали факторы, влияющие на скорость перемещения материала по шнеку; Yuan Tan, Sumira Rashid, Hongbin Liu и др. [6–8] проводили теоретические расчеты параметров транспортирования; M. S. Wang, L. Mei, М. Г. Загоруйко и др. [9–11] проводили имитационное моделирование процесса транспортирования и параметров работы шнеков различных конструкций. При этом анализ данных работ показал, что методика определения производительности и эффективности функционирования шнековых транспортирующих устройств недостаточно универсальна. При описании технологического процесса используются аналитические зависимости, полученные на основании сил, действующих на единичную частицу. Также установлено отсутствие методики определения эффективности функционирования и определения расчетных характеристик для шнековых транспортирующих систем с вращающимся кожухом [12].

Более совершенным для описания процесса транспортировки сыпучей среды является метод дискретных элементов (DEM – Discrete Element Method), имеющий широкое применение в моделировании процессов функционирования рабочих органов сельскохозяйственных машин [13] и позволяющий учитывать не только влияние геометрии транспортирующего рабочего органа (шнека), но взаимовлияние транспортируемых частиц [14; 15].

Данный метод для моделирования процесса транспортировки был использован в разных работах. Ученые [16; 17] исследовали влияние производительности винтового конвейера с помощью метода дискретных элементов. В результате работы было установлено, что DEM моделирование позволяет прогнозировать производительность с точки зрения изменения скорости частиц, степени заполнения, массового расхода, рассеиваемой энергии и потребляемой мощности. Однако в данном исследовании использовались только сферические частицы. Научные коллективы под руководством Z. Ma, S. N. Traore, Yo. Zhu и др. [18; 19], исследовали разгрузку зернового бункера комбайна для уборки риса. С помощью DEM моделирования они определили массовый расход шнеком, который был подтвержден экспериментально. G.-J. Lee, T.-H. Kwon [20] исследовали выгрузку шлама через систему винтовых конвейеров. Ученые рассматривали различные способы задания форм частиц с помощью сферических и мультисферных моделей, а также работу шнека с различным шагом спирали. Исследования показали, что увеличение размера частиц приводит к снижению скорости выгрузки как для сферических частиц, так и для мультисферных частиц приближенной формы. Также в данном исследовании приводится возможность визуализации траектории отдельных частиц. Однако возможность численного анализа данных траекторий отсутствует. L. Sun и др. [21] исследовали влияние наклона спирали шнека на его производительность с использованием DEM моделирования и применения мультисферных частиц. A. Li и др. [22] изучали влияние скорости вращения вертикального шнека и поведение потоков зерна в нем. В работе [23] учеными исследовались динамические характеристики направленного потока материала при перемещении его горизонтальным безжелобовым конвейером. E. Kalay [24], Ya. Lv [25] использовали искусственный интеллект и нейросети для прогнозирования производительности шнекового конвейера. Также важным фактором при проектировании рабочих органов, участвующих в транспортировке, является учет повреждений зерна в процессе уборки [26–28] и транспортировки шнековыми транспортерами [29–31].

С помощью анализа существующих исследований выявлена необходимость формирования общей методики оценки эффективности процесса транспортирования сыпучей среды с использованием шнековых транспортеров путем анализа полученных средних значений коэффициентов пути пройденного частицей к необходимой длине пути, а также затрачиваемой на процесс транспортирования мощности.

Материалы и методы

Для моделирования и исследования процесса перемещения сыпучей массы за основу был взят метод дискретно-элементного моделирования. Данный метод, разработанный Cundall и Strack в 1979 г. [32], позволяет моделировать поток отдельных частиц, имеющих свои собственные размерные характеристики и физико-механические свойства. При перемещении частиц во время моделирования учитываются нормальные и тангенциальные силы, силы гравитации, трения (как между отдельными частицами, так и между частицами и геометрией), имеющие теоретическое обоснование применения [33–35] и верифицированные с использованием лабораторного оборудования [36; 37]. Использование данного метода позволит определить координаты каждой частицы в заданный момент времени, с помощью которых можно построить траектории их перемещения и оценить во сколько раз реальная длина пути, пройденного частицей, отличается от линейной (оптимальной) длины пути в зависимости от свойств транспортируемой сыпучей среды. Коэффициент отношения полного пути, пройденного частицей, к пути вдоль оси шнека позволит оценить эффективность процесса транспортирования.

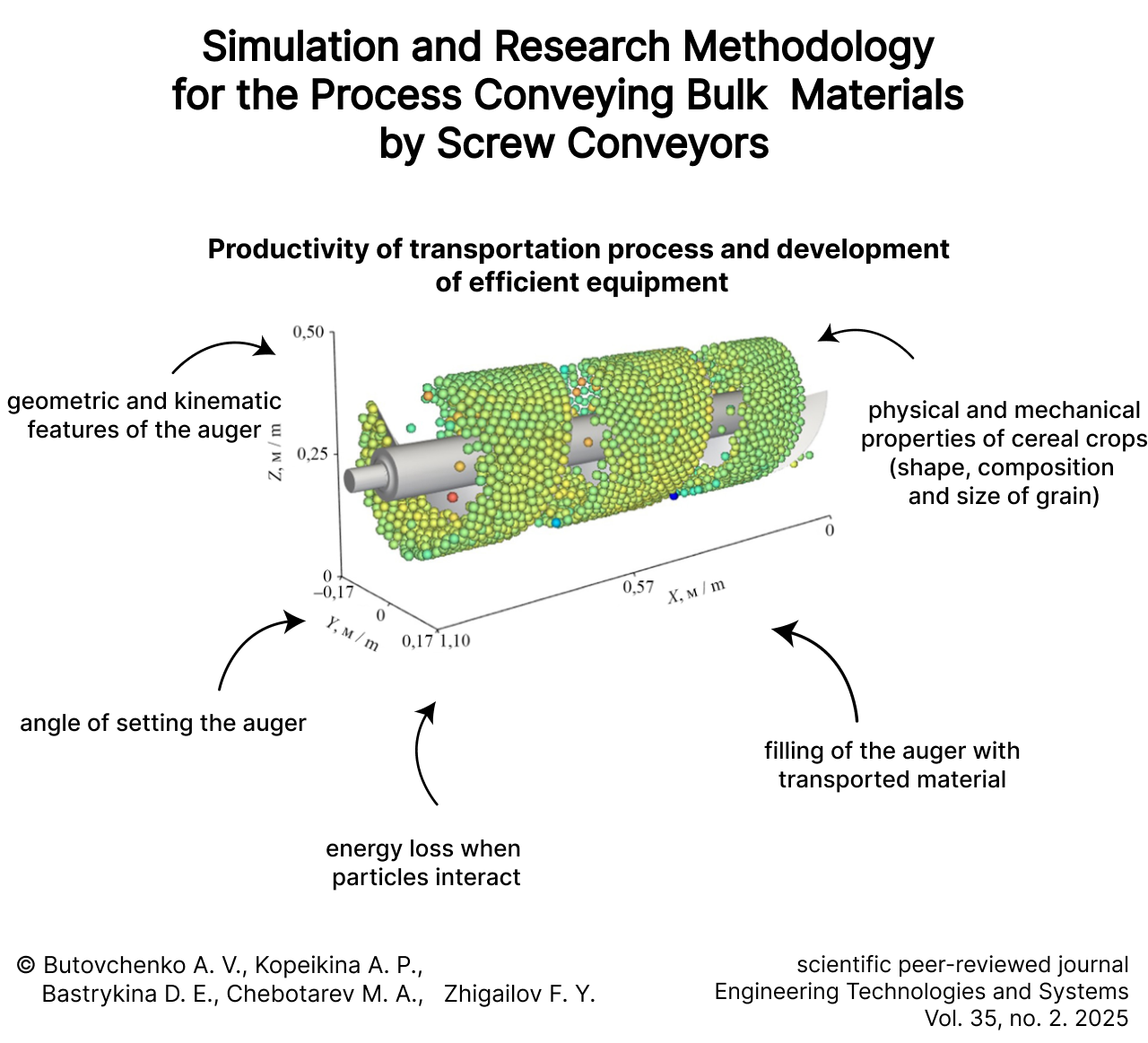
В качестве объекта исследования выбрана система выгрузки зерноуборочного комбайна, представленная на рисунке 1. Данная система имеет в своем составе горизонтальный шнек 5, вертикальный шнек 3 и горизонтальный выгрузной шнек 1.

 

Рис. 1. Модель системы выгрузки зерноуборочного комбайна:
1 – выгрузной шнек; 2 – корпус бункера зерноуборочного комбайна; 3 – вертикальный шнек;
4 – выгрузной раструб; 5 – горизонтальный шнек

Fig. 1. The model of the combine harvester unloading system:
1 – unloading auger; 2 – combine harvester hopper housing; 3 – vertical auger;
4 – unloading bell; 5 – horizontal auger

Источник: здесь и далее рисунки составлены авторами статьи.

Source: hereinafter in this article the figures are made by the authors of the article.

Для отработки методики исследования процесса перемещения сыпучего материала с целью сокращения машинного расчетного времени при необходимости проведения большого количества итерационных расчетов на начальном этапе за основу взяли область горизонтального выгрузного шнека длинной 1 140 мм (рис. 2). Данная область имеет следующие характеристики: наружный диаметр спирали 200 мм; диаметр вала 50 мм; шаг спирали 200 мм; частота вращения шнека 586 мин^–1. Количество транспортируемого материала соответствовало производительности 10 кг/с.

 

Рис. 2. Исследуемая модель секции выгрузного шнека

Fig. 2. Experimental model of the discharge screw conveyer

 

Моделирование процесса транспортирования сыпучей среды осуществлялось с использованием сферических частиц диаметром 8 мм. Физико-механические свойства транспортируемых сельскохозяйственных культур имеют отличия, которые учитывались при постановке задачи и соответствовали эквивалентным свойствам убираемых и транспортируемых культур [33; 38] (табл. 1).

 

Таблица 1. Модели частиц, используемые в DEM

Table 1. Particle models used in DEM

Зерновая культура / Cereal crop	Пшеница / Wheat	Ячмень / Barley	Кукуруза / Corn	Рожь / Rye	Овес / Oats
Насыпная плотность, кг/м3 / Bulk density, kg/m3	770	675	750	675	450
Модуль Юнга, МПа / Young’s modulus, MPa	420	440	315	250	275
Коэффициент Пуассона / Poisson’s ratio	0,420	0,20	0,400	0,19	0,18
Коэффициент статического трения о сталь / Coefficient of static friction on steel	0,445	0,39	0,438	0,28	0,35

 

Используя прикладное программное обеспечение для дискретно-элементного моделирования, на начальном этапе провели моделирование для частиц со свойствами эквивалентными свойствам пшеницы. В результате моделирования получена визуализация процесса перемещения транспортируемых частиц (рис. 3), позволяющая определить координаты каждой частицы в заданный момент времени, что в свою очередь позволило определить путь, пройденный частицей за каждый временной промежуток, и построить траектории движения для каждой отдельно взятой частицы. Пример координат частицы в заданные моменты времени и ее траектория приведены в таблице 2 и на рисунке 4.

 

Рис. 3. Стоп-кадр процесса перемещения частиц пшеницы

Fig. 3. Freeze frame of wheat particle movement process

 

Таблица 2. Координаты траектории частицы пшеницы

Table 2. Coordinates of the wheat particle trajectory

 

Координата частицы X, м / Particle coordinate X, m	Координата частицы Y, м / Particle coordinate Y, m	Координата частицы Z, м / Particle coordinate Z, m	Длина пути, пройденного частицей, м / Length of the path traveled by the particle, m
0,081360861	–0,149816303	0,314328369	0
0,153568341	–0,162920209	0,259280225	0,091738382
0,226103974	–0,153106865	0,193523755	0,190133672
0,299261129	–0,119214529	0,138617870	0,287680154
0,380574551	–0,074177230	0,104766537	0,386605092
0,458907487	–0,024313847	0,088739165	0,480835038
0,531887298	0,026591400	0,088958756	0,569815064
0,601040518	0,085609232	0,111095095	0,663384770
0,666501667	0,138604630	0,163941578	0,762815273
0,735978291	0,161927366	0,229791737	0,861340371
0,804561642	0,155195057	0,300465684	0,960051094
0,875092890	0,117179112	0,363563034	1,062037095
0,945965647	0,059910511	0,401827573	1,160864295
1,012826655	–0,012600411	0,412645043	1,260087507
1,081583013	–0,087486217	0,387709358	1,364763718

 

 

Рис. 4. Траектория частицы пшеницы по длине шнека

Fig. 4. The trajectory of wheat particles along the length of the screw

 

Использование данного дискретно-элементного моделирования применительно к процессу транспортирования сыпучей среды с широкой вариацией технологических свойств позволило визуализировать сам процесс, а также получить информацию о перемещении каждой частицы.

Результаты исследования

В результате моделирования получены координаты транспортируемых частиц в заданные промежутки времени, позволившие построить данные траектории в виде трехмерных графиков и вычислить среднюю длину пути, пройденного частицами. Анализ данных траекторий показал отличные по длине средние значения траекторий перемещения частиц транспортируемой сыпучей среды, имеющих различные исходные физико-механические свойства, соответствующие убираемым и транспортируемым сельскохозяйственным культурам. Расчетная средняя длина пути, пройденная частицами отличающимися физико-механическими свойствами в исследуемой секции выгрузного шнека, составила для пшеницы – 1,581 м, ячменя – 1,557 м, кукурузы – 1,764 м, ржи – 1,564 м, овса – 1,595 м.

В процессе транспортирования частицы не равномерно распределяются по объему, образуются микросводы, поэтому для получения лучшего представления о процессе перемещения использовали Эйлеровую статистику, позволяющую визуализировать суммарную массу частиц, проходящих в задаваемых для исследования сечениях. Результаты применения данного инструмента визуализации для оценки распределения частиц по сечениям представлены на рисунке 5.

 

Рис. 5. Сумма массы частиц пшеницы в различных сечениях

Fig. 5. The sum of the mass of wheat particles according to Eulerian statistics

 

Поведение частицы транспортируемой сыпучей среды можно описать через уравнения траектории ее движения. Существуют различные методики описания данных траекторий. В первом варианте траекторию движения частицы (рис. 4), которая визуально представляет собой синусоиду, опишем системой математических уравнений, используя следующий вид шаблонной функции:

$\left\{\begin{array}{c}y=A\cdot \cos (F(x))\\ z=A\cdot \sin (F(x))\end{array}\right.$                                                  

где х, у, z – координаты точек траектории движения частицы, м; А – безразмерный коэффициент.

По гипотезе оптимальная траектория частицы должна быть близка к линейной, поэтому последовательно рассмотрены три ее возможных варианта:

 $F(x)=B+Cx;$                                                                                                  

 $F(x)=B+Cx+D{x}^2;$                                                                                     

$F(x)=B+Cx+D{x}^2+E{x}^3.$                                                                          

где х – координата траектории частицы, м; А, B, C, D, E – безразмерные коэффициенты.

Качество аппроксимации было проверено по двум показателям: коэффициенту корреляции и среднеквадратичному отклонению в узловых точках. В данном случае под узловыми точками были приняты расчетные координаты точек движения частицы в заданные промежутки времени, представленные в таблице 2. Для нахождения коэффициентов модели A, B, C, D, E воспользовались эквивалентным методом, состоящим в минимизации невязки:

${\displaystyle \sum _{i=1}^n{(y_i-A\cdot \cos (F(x_i)))}^2+(z_i-A}\cdot \sin (F(x_i)){)}^2\to \min .$

После проведения вычислений с использованием Mathcad для уравнений было установлено, что наиболее оптимально данную траекторию можно описать аппроксимирующей функцией:

$\left\{\begin{array}{l}y=\mathrm{0,14405}\cdot \cos (-\mathrm{1,9481}+\mathrm{7,4981}x)\\ z=\mathrm{0,14405}\cdot \sin (-\mathrm{1,9481}+\mathrm{7,4981}x).\end{array}\right.$

Коэффициент корреляции при этом составил 0,996.

Во втором варианте траекторию движения частицы, представленную на рисунке 4, можно описать с помощью уравнения, полученного на основе кубической регрессии:

 $\begin{array}{l}z=-\mathrm{2,772}x+\mathrm{1,773}y-\mathrm{7,516}{x}^2+\mathrm{2,047}xy+\mathrm{3,632}{y}^2-\\ -\mathrm{4,968}{x}^3-\mathrm{1,642}{x}^{2}y+\mathrm{7,48}x{y}^2-\mathrm{3,662}{y}^3-\mathrm{0,113.}\end{array}$                                        

Коэффициент корреляции при этом составил 0,9998.

В обоих вариантах получены близкие по значению коэффициенты корреляции. Следовательно, оба подхода для описания траектории частицы являются равнозначными.

Для определения эффективности процесса транспортирования частиц был использован коэффициент отношения полного пути, пройденного частицей к пути вдоль оси шнека:

$k=\frac{l}{S},$                                                          

где l – среднее значение полной длины пути, пройденного частицей, м; S – путь частицы, пройденный вдоль оси шнека, м.

Для сферических частиц со свойствами эквивалентными свойствам пшеницы средняя длина пути l составила 1,581 м (табл. 3), при этом путь вдоль оси шнека S составил 1,14 м (данное значение соответствует длине исследуемой секции и максимальной координате X):

$k=\frac{\mathrm{1,581}}{\mathrm{1,14}}=\mathrm{1,387.}$

Используя данную методику, был определен коэффициент отношения пройденного пути к пути вдоль оси для сферических частиц со свойствами эквивалентными свойствам других культур.

 

Таблица 3. Коэффициенты отношения пройденного пути к пути вдоль оси

Table 3. Coefficients of the ratio of the traveled path to the path along the axis

Культура / Crop	Среднее значение длины пути, пройденного частицей l, м / Average value of the path length traveled by the particle l, m	k
Пшеница / Wheat	1,581	1,387
Ячмень / Barley	1,557	1,366
Кукуруза / Corn	1,764	1,548
Рожь / Rye	1,564	1,372
Овес / Oats	1,595	1,399

 

 

Анализ результатов моделирования показал, что при одинаковой частоте вращения шнека, но разных физико-механических свойствах длина пути частиц одного размера будет различна, следовательно, энергия для перемещения этих частиц также будет отличаться.

Существующие методики определения мощности основаны на аналитическом определении мощности, необходимой на транспортировку сыпучей среды шнековыми транспортирующими устройствами. Однако данные зависимости не учитывают широкую вероятность свойств транспортируемого материала, особенности геометрии и условий эксплуатации, а также длину траектории пути, пройденного частицей. При моделировании процесса транспортирования с использованием метода дискретно-элементного моделирования возможно получить значения крутящего момента, действующие на привод шнека. Пример полученных расчетных значений в заданном исследуемом промежутке времени представлен на рисунке 6. Используя данные значения, можно определить среднее значение крутящего момента, действующего на привод шнека. Полученные расчетные средние значения крутящего момента по культурам с различными физико-механическими свойствами и траекториями движения представлены в таблице 4.

 

Рис. 6. Расчетные значения крутящего момента, приложенного к шнеку при транспортировке пшеницы в промежутке времени исследования

Fig. 6. Calculated values of torque applied to the screw during wheat transportation in the study time interval

Необходимую на привод шнека мощность при транспортировке зерновой массы различных культур определим, используя следующее выражение:

 $P=\frac{n\cdot \overline{M}}{9550},$                                                  

где $\overline{M}$ – среднее значение крутящего момента за исследуемый промежуток времени, Нм; n – частота вращения, мин^–1.

Определим мощность, необходимую на привод шнека при транспортировке пшеницы:

$P=\frac{586\cdot \mathrm{54,3}}{9550}=\mathrm{3,33}\text{\hspace{0.33em}кВт.}$

Аналогичным образом определена расчетная мощность на привод шнека для транспортировки других культур. Полученные значения приведены в таблице 4.

 

Таблица 4. Среднее значение крутящего момента и мощности, необходимой на привод шнека, в зависимости от транспортируемой культуры

Table 4. Average torque and power required to drive the screw depending on the crop being transported

Культура / Crop	Среднее значение крутящего момента , Нм / Average torque value , Nm	Мощность на привод шнека Р, кВт / Power for the screw drive P, kW
Пшеница / Wheat	54,30	3,33
Ячмень / Barley	43,78	2,69
Кукуруза / Corn	70,89	4,34
Рожь / Rye	50,10	3,07
Овес / Oats	59,10	3,63

 

В результате исследования процесса транспортирования были получены средние расчетные значения длины траекторий частиц в зависимости от их физико-механических свойств. Используя значения координат характерных точек траектории одной из частиц пшеницы, были получены два вида уравнений, равнозначно описывающих характер движения исследуемой частицы в зависимости от ее физико-механических свойств, геометрических размеров и кинематических режимов функционирования шнекового транспортера. Полученные в результате имитационного моделирования данные позволили определить мощность, затрачиваемую на перемещение частиц с различными физико-механическими свойствами.

Обсуждение и заключение

Предлагаемая методика исследования транспортирования сыпучей среды шнеком с учетом влияния физико-механических свойств зерновых культур на процесс транспортировки выгрузным шнеком зерноуборочного комбайна позволяет учитывать разнообразные факторы, включая форму, состав и размеры зерна, геометрические и кинематические особенности шнека, угол его установки, заполненность шнека транспортируемым материалом, а также потери энергии при взаимодействии частиц. Данная методика существенно повышает точность получаемой при моделировании информации. Такой подход позволяет оценивать продуктивность процесса транспортировки и разрабатывать более эффективные конструкции оборудования.

Использование данного подхода позволило провести моделирование процесса транспортирования шнеком зернового вороха, имеющего различные физико-механические свойства. В результате моделирования были получены средние значения траекторий транспортируемых частиц в исследуемом участке шнека длиной 1 140 мм, наружным диаметром спирали 200 мм, диаметром вала 50 мм, шагом спирали 200 мм. Частота вращения шнека составила 586 мин ^–1 при расчетной производительности 10 кг/с. Используя средние значения траекторий пройденного пути, были определены коэффициенты отношения пройденного пути к пути вдоль оси для сферических частиц со свойствами эквивалентными свойствам других культур: для пшеницы – 1,387; ячменя – 1,366; кукурузы – 1,548; ржи – 1,372; овса – 1,399. Анализ значений данных коэффициентов показывает, что путь, проходимый частицей, больше необходимого в 1,366–1,548 раз. Полученные в процессе моделирования значения крутящего момента позволили определить расчетную мощность, необходимую на привод шнека и составившую для пшеницы 3,33 кВт; ячменя – 2,69 кВт; кукурузы – 4,34 кВт; ржи – 3,07 кВт; овса – 3,63 кВт. Анализ полученных значений позволяет выявить взаимосвязь коэффициента отношения пройденного пути к пути вдоль оси и необходимой на процесс транспортирования мощности. Чем больше коэффициент, тем выше необходимая на транспортирование мощность. Предложенная методика может быть использована для сравнительной оценки шнеков, имеющих различные конструктивные характеристики, или при транспортировании сыпучей среды с разными физико-механическими свойствами.

 

¹ Справочник конструктора сельскохозяйственных машин / под ред. М. И. Клецкин. 4 т. М. : Машиностроение, 1967. Т. 1. 722 с.

² ГОСТ 2037-82. Конвейеры винтовые стационарные общего назначения. Общие технические условия. М. : Издательство стандартов, 1982.

³ DIN 15261-1-1986. Continuous Mechanical Handling Equipment for Loose Bulk Materials; Screw Conveyors; Mating Dimensions [Электронный ресурс]. URL: https://nd.gostinfo.ru/document/4027408.aspx (дата обращения: 23.09.2024); DIN 15261-2-1986. Continuous Mechanical Handling Equipment for Loose Bulk Materials; Screw Conveyors; Helical Screw Blade [Электронный ресурс]. URL: https://nd.gostinfo.ru/document/4023257.aspx (дата обращения: 23.09.2024).

⁴ DIN 15262-1983. Continuous Mechanical Handling Equipment; Screw Conveyors for Loose Bulk Materials; Design Principles [Электронный ресурс]. URL: https://www.standards.ru/document/4038442.aspx (дата обращения: 23.09.2024).

⁵ ISO 7119-1981. Continuous Mechanical Handling Equipment for Loose Bulk Materials – Screw Conveyors – Design Rules for Drive Power [Электронный ресурс]. URL: https://clck.ru/3KHfcw (дата обращения: 23.09.2024).

About the authors

Andrey V. Butovchenko

Don State Technical University

Author for correspondence.
Email: butovchenkoav@yandex.ru
ORCID iD: 0000-0002-9335-9586
ResearcherId: N-4962-2016

Dr.Sci. (Eng.), Professor of the Rostselmash Institute of Advanced Mechanical Engineering

Russian Federation, 1 Gagarin Square, Rostov-on-Don 344000

Anastasia P. Kopeikina

Don State Technical University

Email: kopeikina_bstu@mail.ru
ORCID iD: 0009-0005-9015-0401
ResearcherId: LTE-5264-2024

Postgraduate Student of the Rostselmash Institute of Advanced Mechanical
Engineering

Russian Federation, 1 Gagarin Square, Rostov-on-Don 344000

Daria E. Bastrykina

Don State Technical University

Email: bastrykina.dasha.00@mail.ru
ORCID iD: 0009-0007-8076-0980
ResearcherId: LSJ-4507-2024

Postgraduate Student of the Rostselmash Institute of Advanced Mechanical
Engineering

Russian Federation, 1 Gagarin Square, Rostov-on-Don 344000

Mikhail A. Chebotarev

Don State Technical University

Email: mchibis1997@gmail.com
ORCID iD: 0009-0008-5362-6142
ResearcherId: LSJ-4505-2024

Postgraduate Student of the Rostselmash Institute of Advanced Mechanical
Engineering

Russian Federation, 1 Gagarin Square, Rostov-on-Don 344000

Fedor Yu. Zhigailov

Don State Technical University

Email: 3Fedor_Zhigaylov_Sr_3@mail.ru
ORCID iD: 0009-0000-0687-4225
ResearcherId: LSJ-3558-2024

Master’s Student of the Rostselmash Institute of Advanced Mechanical Engineering

Russian Federation, 1 Gagarin Square, Rostov-on-Don 344000

References

Supplementary files